数学-2023年管理类联考数学练习19

　　问题求解：

　　1、等差数列{a_n}满足a₁=8,a₂+a₄=a₁，则前n项和最大值为( )

　　A.16

　　B. 17

　　C.18

　　B.19

　　E.20

　　2、已知实数x满足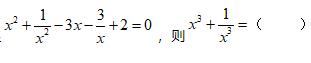，则

　　A.12

　　B.15

　　C.18

　　D.24

　　E.27

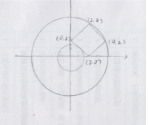
　　3、设实数x,y满足|x-2|+|y-2|≤2，则x₂₊y₂的取值范围是( )

　　A.[2,18]

　　B.[2,20]

　　C.[2,36]

　　D.[4,18]

　　E.[4,20]

　　1.【答案】E

　　【解析】a₁=8，a₂+a₄=8，a₃=4,d=-2，a₃=0，所以S4=S5=8+6+4+2+0=20

　　2.【答案】C

　　【解析】根据完全平方公式化简:(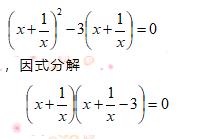，因式分解，所以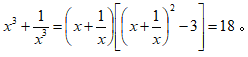

　　(18这个数字2014年真题出现过一模一样的)。

　　3.【答案】B

　　【解析】画图，最小值点在与直线x+y=2相切，在(1,1)点取最小值，最大值点是x+y=6的端点值(2,4)或(4,2),所以范围是2≤x₂+y₂≤20